原子核物理概论

原子核的基本性质

原子核的组成

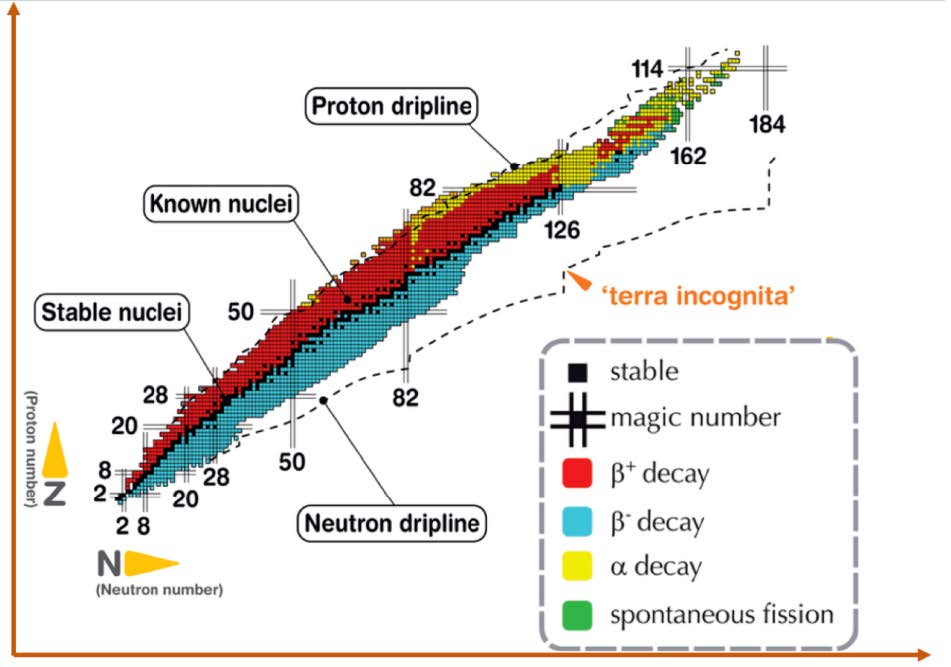
1. $\beta$ 稳定线: $$\begin{equation} Z = \frac{A}{1.98 + 0.015 A^{2/3}} \end{equation}$$

轻核区，库仑作用影响小，泡利不相容原理主导，中子和质子都是费米子，每个能态最多容纳两个中子和两个质子 ，体系能量最低时 $N = Z$；

重核丰中子，因质子数增多时质子间库仑排斥能增长比核力快，需增加中子数、减少质子数来降低库仑力破坏作用，维持原子核稳定并使其处于低能量状态。

1. 原子核的结合能:

   $$\begin{equation} B = (Z m_p + N m_n - m_X) c^2 = [Z M_H + (A - Z) m_n - M_X] c^2 \end{equation}$$

2. 比结合能:

   $$\begin{equation} \epsilon = \frac{B}{A} \end{equation}$$

[Image of binding energy per nucleon curve]

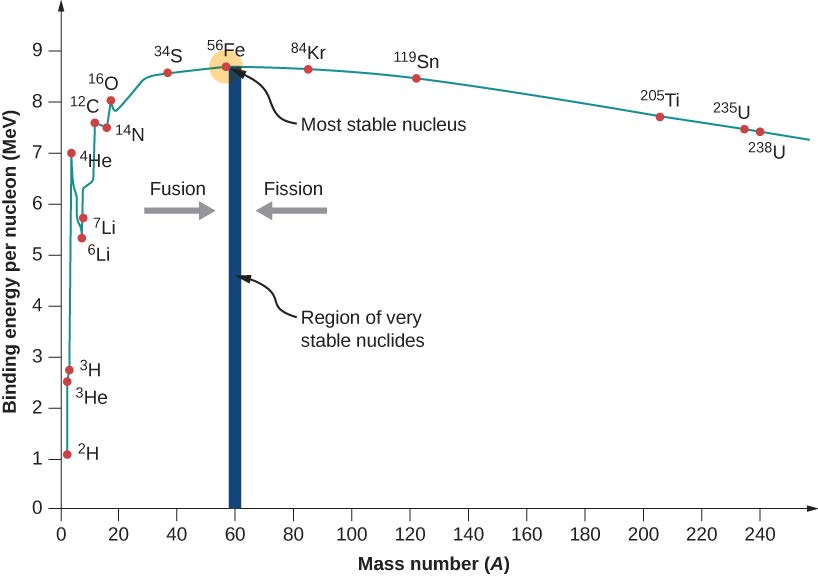
轻核 ($A < 30$) 比结合能随质量数增大呈周期性变化，峰值在 $A$ 为 $4$ 整数倍处，对应质子数和中子数相等的偶偶核 ；中间核素（$30 < A < 120$）比结合能近似常数，${}^{56}\text{Fe}$ 核比结合能最大为 $8.8 \text{ MeV}$ ；重核（$A > 200$）比结合能小 。

比结合能曲线表明轻核和超重核不如中间核素稳定，轻核可通过聚变、重核可通过裂变释放能量。

1. 原子核半径与质量数 $$\begin{equation} R = r_0 A^{\frac{1}{3}} \quad (r_0 = 1.20 \text{ fm}) \end{equation}$$ 原子核的密度是常数 $$\begin{equation} \rho = \frac{M}{V} = \frac{M}{\frac{4}{3} \pi R^3} = \frac{A u}{\frac{4}{3} \pi r_0^3 A} \quad \text{约 } 2 \text{ 亿吨/厘米}^3 \end{equation}$$ 核物质是密度很高、不易压缩的 “液滴”

核力

原子核由质子和中子组成，核子间的强相互作用力即核力，能将核子紧密结合成高密度原子核。

性质

1. 短程力：力程在 $\text{fm}$ 量级（$1\text{fm} = 10^{-15}\text{m}$），仅存在于几个 $\text{fm}$ 范围内 ，如 $\alpha$ 粒子散射实验可证明。

2. 饱和性：原子核结合能近似与质量数 $A$ 成正比，比结合能 $B/A$ 不随 $A$ 增加而增加，体现核子仅与相邻核子作用。

3. 电荷无关性：在核力力程内，质子-质子、质子-中子、中子-中子间强相互作用相似。

4. 极短范围排斥力：核子间距 $0.8-2\text{fm}$ 时表现吸引力，小于 $0.8\text{fm}$ 表现排斥力，大于 $10\text{fm}$ 核力为零。

5. 自旋相关性：两核子自旋平行与反平行时相互作用不同。

   自然界中氘核的自旋为 1，说明质子和中子自旋平行时，核力较强，结合能大。

6. 此外，核力有少量非中心力和多体力成分，反映核子内部微观结构，核子由夸克构成，夸克间通过传递胶子相互作用，相关理论为量子色动力学。

   库伦相互作用：交换虚光子，力程较长。

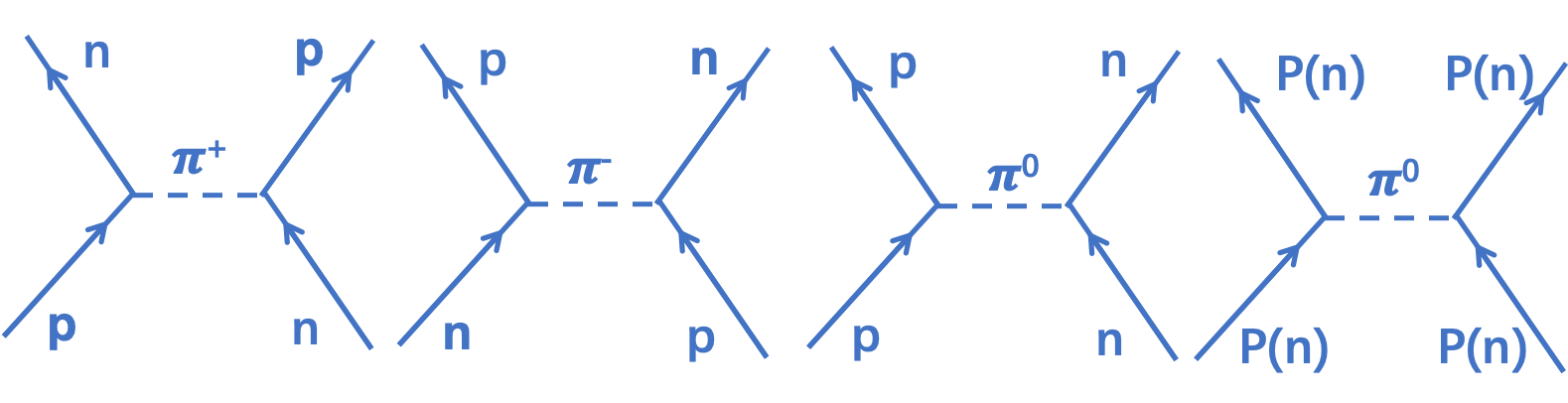
   介子理论：认为核子间相互作用通过交换介子而产生的。由不确定关系和力程可得出介子质量。

核自旋

中子和质子都是费米子，与电子一样其自旋量子数为 1/2。

• 偶偶核， $I=0$，如 $\text{C, O}$ 原子核
• 奇奇核， $I$ 为整数
• 奇偶核， $I$ 为半整数，如质子

1. 质子的自旋磁矩:

   $$\begin{equation} \mu_p = g_p \frac{e}{2 m_p} s_p, \quad g_p = 5.586 \end{equation}$$

2. 中子的自旋磁矩:

   $$\begin{equation} \mu_n = g_n \frac{e}{2 m_p} s_n, \quad g_n = -3.82 \end{equation}$$

3. 原子核的自旋磁矩:
   原子中所有核子的自旋角动量和轨道角动量的矢量和构成原子核的总角动量 $\mathcal{I}$ ；核磁矩同理。

   核磁矩远小于原子磁矩。

   $$\begin{equation} \mu_I = g_I \frac{e}{2 m_e} \mathcal{I} \end{equation}$$

4. 原子核自旋磁矩的大小:

   $$\begin{equation} \mu_I = g_I \sqrt{I(I + 1)} \mu_N \end{equation}$$

5. 原子核自旋磁矩 $z$ 分量的大小:

   $$\begin{equation} \mu_{Iz} = g_I m_I \mu_N \end{equation}$$

   此处 Bohr 磁子 (核磁子) $\mu_N = \frac{e \hbar}{2 m_p}$

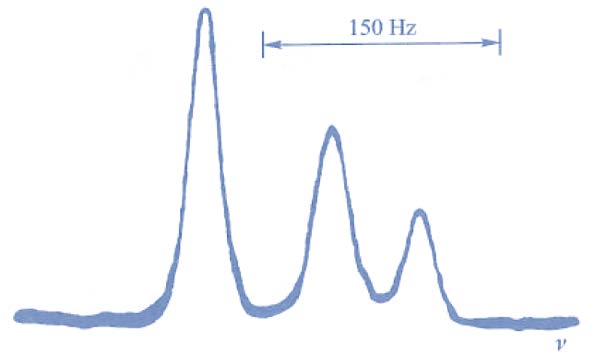
核磁共振 (NMR)

1. $$\begin{equation} U = -\mu_I \cdot B = -g_I m_I \mu_N B \end{equation}$$

   自旋角动量与磁场方向反平行的质子能级高。

2. 核磁共振:

   $$\begin{equation} \Delta E = g_I \mu_N B = h \nu \end{equation}$$

3. 化学移位：乙醇分子三个原子团中的 $\text{H}$ 核共振。

   

原子的超精细结构

产生超精细结构的一个重要原因就是核外电子的运动产生的磁场与原子核的磁矩发生磁偶极相互作用产生附加势能。

1. 原子体系的总角动量: $$\begin{equation} \mathcal{F} = \mathcal{I} + \mathcal{J} \end{equation}$$
2. 原子体系总角动量的大小: $$\begin{equation} \mathcal{F} = \sqrt{F(F + 1)} \hbar \end{equation}$$
3. 原子核的附加能量（均值）: $$\begin{equation} \Delta E = A \mathcal{I} \cdot \mathcal{J} = \frac{A}{2} [F(F + 1) - I(I + 1) - J(J + 1)] \hbar^2 \end{equation}$$

   21cm 氢线

   来自于氢原子基态超精细能级之间的跃迁。对应光子波长为 $21\text{cm}$。

原子核结构模型

液滴模型

考虑到原子核密度、比结合能均近似为常数。
魏扎克公式

原子核的结合能

$$\begin{equation} E_{\mathrm{B}} = a_{\mathrm{V}} A - a_{\mathrm{S}} A^{2/3} - a_{\mathrm{C}} Z(Z - 1) A^{-1/3} - a_{\mathrm{Sym}} (Z - N)^2 A^{-1} + E_{\mathrm{BP}} \end{equation}$$

• $a_{\mathrm{V}} A$：体积能项

• $a_{\mathrm{S}} A^{2/3}$ ：表面能项，因处于表面的核子与内部核子的相互作用情况不同

• $a_{\mathrm{C}} Z(Z - 1) A^{-1/3}$：库仑能项，质子间库仑排斥力使结合能减小。

• $a_{\mathrm{Sym}} (Z - N)^2 A^{-1}$ ：对称能项，核内质子数与中子数相等时，对称能等于零；否则由于泡利不相容原理，当核内一种核子多于另一种核子时就要花费较多的能量。

• $E_{\mathrm{BP}}$：对能项，是考虑到原子核中质子和中子的配对更稳定。

  $$E_{\mathrm{BP}} = \begin{cases} a_{\mathrm{p}} A^{-1/2} & \text{ 偶偶核} \\ 0 & \text{ 奇 } A \text{ 核} \\ -a_{\mathrm{p}} A^{-1/2} & \text{ 奇奇核} \end{cases} \quad a_{\mathrm{p}} = 11.2 \text{ MeV}$$

  它表明，偶偶核最稳定，奇奇核最不稳定。

壳层模型

• 存在幻数核，即当原子核内的质子数或中子数为 2, 8, 20, 28, 50, 82 和 126 时核特别稳定。
• 丰度高，结合能大。
  $\rightarrow$（近独立粒子模型）
• 假设核内每个核子都在由其它核子提供的平均势场中作相对独立运动 (中心力场下的近独立粒子近似)。
• 求解核子薛定谔方程。
  $\rightarrow$波函数、宇称、核自旋。
  $\rightarrow$原子核的壳层结构。

核子的 $\mathcal{LS}$ 耦合给出了全部幻数，解释了大多数原子核基态的自旋和宇称。

集体模型

考虑个体核子的运动和集体的运动互相结合，原子核内部运动较全面的描述 - 核子互相吸引，形成一个集体，有集体振动，转动。

• 核子是在一个变动的势场中。

集体模型可以描述 原子核形变、核的集体振动、原子核的转动。

核衰变

核衰变的一般规律

1. 指数衰变: $$\begin{equation} N = N_0 e^{-\lambda t} \end{equation}$$ $\lambda$ 称为衰变常数。
2. 半衰期: $$\begin{equation} T_{\frac{1}{2}} = \frac{\ln 2}{\lambda} = \frac{0.693}{\lambda} \end{equation}$$
3. 平均寿命: $$\begin{equation} \tau = \frac{1}{N_0} \int_0^{+\infty} t \lambda N \, dt = \int_0^{+\infty} t \lambda e^{-\lambda t} \, dt = \frac{1}{\lambda} = \frac{T_{\frac{1}{2}}}{\ln 2} \end{equation}$$
4. 放射性活度（衰变率）: $$\begin{equation} A = -\frac{\mathrm{d}N}{\mathrm{d}t} = \lambda N_0 e^{-\lambda t} = A_0 e^{-\lambda t} = \lambda N \end{equation}$$ 放射性活度单位: Bq (贝克勒尔)。 $1\text{s}$ 内有 1 个核衰变，放射性活度就是 $1\text{Bq}$，$1\text{Bq} = 1\text{s}^{-1}$。

例：活着的有机体中，${}^{14}\text{C}$ 与 ${}^{12}\text{C}$ 的数量比在大气中是相同的，约为 $1.3 \times 10^{-12}$。有机体死亡后，由于 ${}^{14}\text{C}$ 的放射性衰变，${}^{14}\text{C}$ 的含量就不断减少，因此，测量每克碳的衰变率就可计算有机体的死亡时间。现测得：取之于某一受骨的 $100\text{g}$ 碳的 $\beta$ 衰变率为 $300$ 次衰变/$\text{min}$，试问该骸骨已有多久历史？(${}^{14}\text{C}$ 的半衰期为 $5730\text{a}$)

解：在活的有机体 ($100\text{g}$) 碳中 ${}^{14}\text{C}$ 的核数为

$$N_0 = \frac{100}{12}\text{mol} \times 6.02 \times 10^{23}\text{mol}^{-1} \times 1.3 \times 10^{-12} = 6.52 \times 10^{12}$$

放射性活度为

$$A_0 = \lambda N_0 = \frac{\ln 2}{T_{1/2}}N_0$$

根据 $A = A_0 e^{-\lambda t}$，可得

$$t = \frac{1}{\lambda}\ln\frac{A_0}{A} = 1.33 \times 10^{4} \text{ a}$$

$\alpha$ 衰变

1. $\alpha$ 衰变: $$\begin{equation} {}^A_Z X \longrightarrow {}^{A-4}_{Z-2} Y + \alpha \end{equation}$$

2. $\alpha$ 衰变能:

   $$\begin{equation} Q(\alpha) = (m_X - m_Y - m_\alpha) c^2 = [M_X - (M_Y + M_{\text{He}})] c^2 \end{equation}$$

   $\alpha$ 衰变发生条件，即 $Q(\alpha) > 0$。

3. $\alpha$ 衰变能和 $\alpha$ 粒子动能之间的关系:

   $$\begin{equation} Q(\alpha) = E_Y^k + E_\alpha^k = \left(1 + \frac{m_\alpha}{m_Y}\right) E_\alpha^k \approx \frac{A}{A-4} E_\alpha^k \end{equation}$$

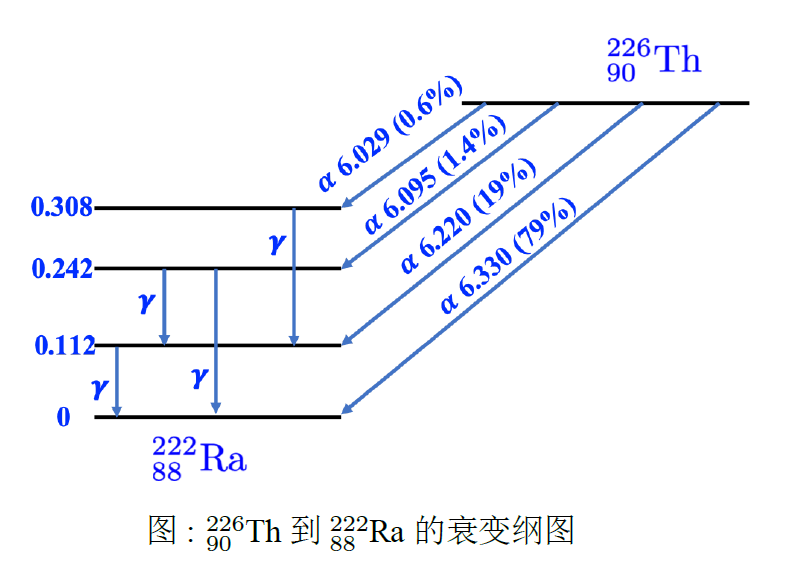
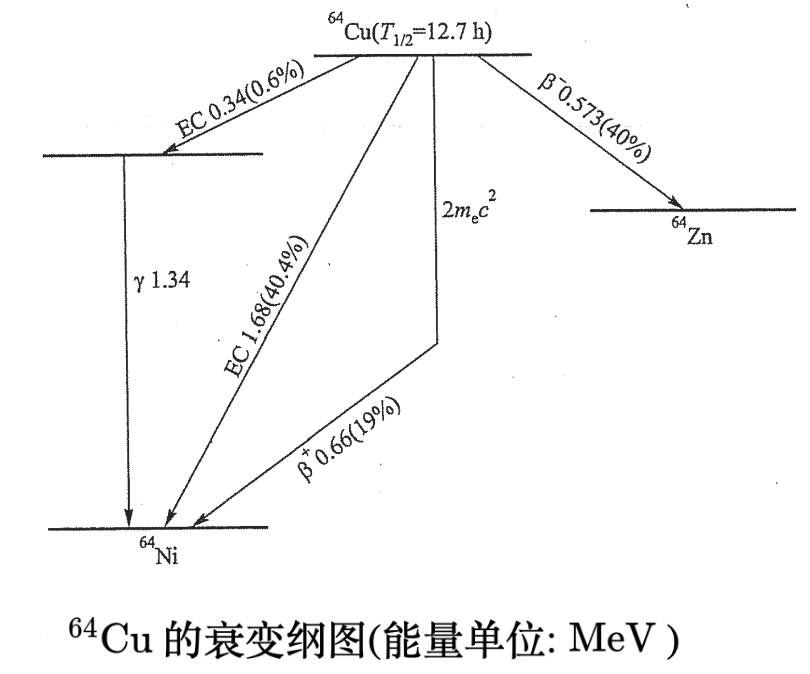
   $E_\alpha$ 测量值为离散值，预示着子核具有分立的能级。放出的 $\alpha$ 粒子的能量最大的一组，说明衰变到了基态，对于放出其他能量的 $\alpha$ 粒子的情况，说明衰变到了激发态。

画衰变纲图时通常把原子序数大的核素放在右边，箭头指向左下为 $\alpha$、$\beta^+$ 衰变，箭头指向右下为 $\beta^-$ 衰变，箭头垂直向下的为 $\gamma$ 衰变；在跃迁线的旁边注明衰变类型、发射粒子的动能和相对强度（分支比）；每条能级旁注明能量、半衰期和状态量子数。

$\beta$ 衰变

衰变产物有三个粒子：子核、电子、（反）中微子，衰变能就可以在三个粒子之间分配。因为子核质量远大于电子和（反）中微子的质量，所以子核携带的反冲动能只占了衰变内非常小的一部分，大部分能量在电子和（反）中微子之间分配。实验上仅测量了电子的能谱，就显示出了连续的能谱。

由于质子的质量小于中子的质量，故自由状态的质子不可能自发衰变为中子，而在原子核内的质子，因为泡利原理的存在及核子之间的相互作用使得能量在核子间重新分配。

1. $\beta^-$ 衰变: $$\begin{equation} {}^A_Z X \longrightarrow {}^A_{Z+1} Y + e^- + \bar{\nu}_e \end{equation}$$
2. $\beta^-$ 衰变能: $$\begin{equation} Q(\beta^-) = (m_X - m_Y - m_e) c^2 = (M_X - M_Y) c^2 \end{equation}$$ 衰变能的表达式中忽略了电子在原子中结合能的差异。
3. $\beta^+$ 衰变: $$\begin{equation} {}^A_Z X \longrightarrow {}^A_{Z-1} Y + e^+ + \nu_e \end{equation}$$
4. $\beta^+$ 衰变能: $$\begin{equation} Q(\beta^+) = (m_X - m_Y - m_e) c^2 = (M_X - M_Y - 2 m_e) c^2 \end{equation}$$
5. 电子俘获 (EC): $$\begin{equation} {}^A_Z X + e^- \longrightarrow {}^A_{Z-1} Y + \nu_e \end{equation}$$
6. 电子俘获能: $$\begin{equation} Q(i) = (m_X + m_e - m_Y) c^2 - W_i = (M_X - M_Y) c^2 - W_i \end{equation}$$

$\gamma$ 衰变

(经 $\alpha, \beta$ 衰变形成的) 激发态核通过发射 $\gamma$ 光子跃迁到低激发态或基态。

1. $\gamma$ 光子的能量 ($E_R$ 为子核反冲能): $$\begin{equation} E_\gamma = h \nu = \Delta E - E_R \end{equation}$$

2. 核跃迁或不放出光子，其能量直接使电子脱离原子：

   内转换电子的能量 ($B_i$ 为内转换电子在原子中的结合能):

   $$\begin{equation} E_e = \Delta E - B_i - E_R \end{equation}$$

   内转换电子释放出来后，原子壳层中便出现一个空位，当外层电子向这个空位跃迁时，多余的能量或以 X 射线的形式放出，或产生俄歇电子。

Mössbauer 效应

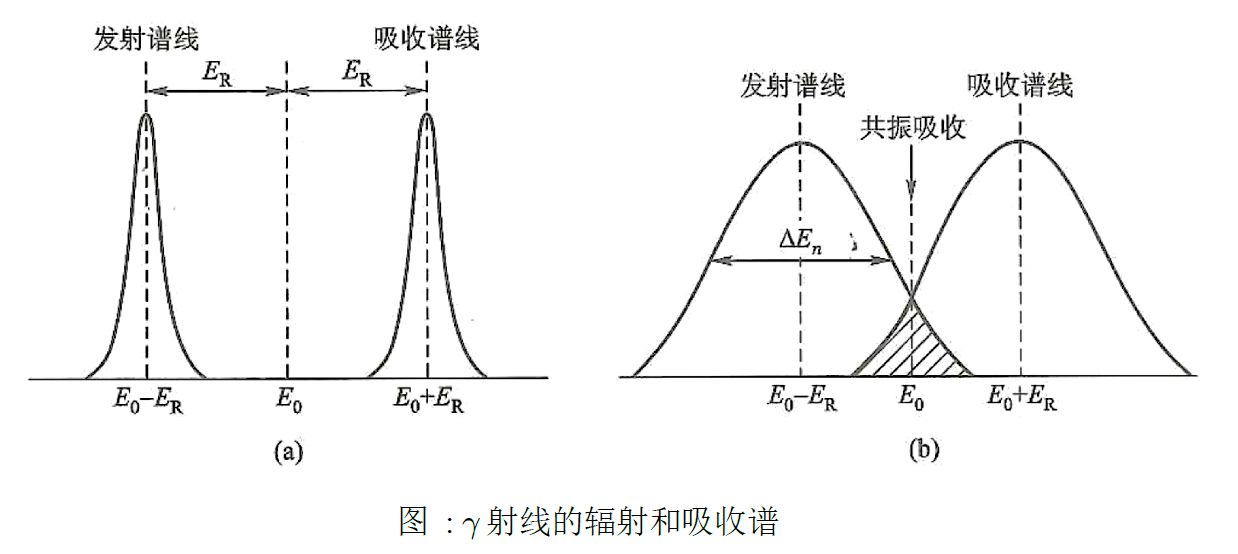
从原子核激发态跃迁到基态所放射出的 $\gamma$ 射线被处于基态的另一个同类原子核吸收，并使它跃迁到激发态的现象称为原子核的共振吸收。条件是原子核退激过程中所放出的 $\gamma$ 射线的能量与同一原子核受激过程所吸收的能量完全相等。

1. 谱线自然宽度: $$\begin{equation} \Delta E_n = \frac{\hbar}{\tau} \end{equation}$$
2. 核反冲能: $$\begin{equation} E_R = \frac{p_\gamma^2}{2M} = \frac{(\Delta E)^2}{2Mc^2} \end{equation}$$
3. 核从激发态跃迁到基态放出光子能量: $$\begin{equation} E_{\gamma E} = \Delta E - E_R \end{equation}$$

4. 核从基态跃迁到激发态吸收光子能量:

   $$\begin{equation} E_{\gamma X} = \Delta E + E_R \end{equation}$$

   

5. Mössbauer 效应（设法减少反冲能，实现无反冲 $\gamma$ 共振吸收）:

   $$\begin{equation} \Delta E_n \gg E_R \end{equation}$$

   穆斯堡尔无反冲共振吸收实验装置中，由于多普勒效应，吸收体吸收到的 $\gamma$ 光子的频率为

   $$\begin{equation} \nu' = \nu \left(1 + \frac{v}{c}\right) \end{equation}$$

   其相应的能量为

   $$\begin{equation} E' = E_0 \left(1 + \frac{v}{c}\right) \end{equation}$$

核反应、核裂变与核聚变

核反应

1. 核反应:

   $$\begin{equation} i + T \longrightarrow l + R \end{equation}$$ $$\begin{equation} \text{或 } T(i, l)R \end{equation}$$

   $i, T, l$ 和 $R$ 代表入射粒子，靶核，出射轻粒子，剩余核。

2. 反应能:

   $$\begin{equation} Q = (m_i + m_T - m_l - m_R)c^2 = E_l^k + E_R^k - E_i^k \end{equation}$$

   如果 $Q > 0$，称放能反应； $Q < 0$，则称吸能反应。

3. $Q$ 方程:

   $$\begin{equation} Q = \left(1 + \frac{m_l}{m_R}\right)E_l^k - \left(1 - \frac{m_i}{m_R}\right)E_i^k - \frac{2\sqrt{m_i m_l E_i^k E_l^k}}{m_R} \cos \theta \end{equation}$$

核裂变

1. 自发裂变与诱发裂变
2. 链式反应
   若要使天然铀发生中子诱发的链式裂变反应，可采取以下措施：
   • 减小铀中的杂质含量，增加 ${}^{235}\text{U}$ 的百分比（即所谓浓缩铀）；
   • 加大铀的体积或提高铀的密度，使其大于临界反应值；
   • 在铀中加减速剂（如重水或石墨）使快中子减速成热中子。
3. 反应堆

核聚变

1. 太阳的热核聚变：碳循环、质子-质子循环 $$\begin{equation} 4p \longrightarrow \alpha + 2e^+ + 2\nu + 26.7 \text{ MeV} \end{equation}$$

2. 氢弹的热核聚变:

   $$\begin{equation} {}^6\text{Li} + n \longrightarrow {}^3\text{H} + {}^4\text{He} + 4.9 \text{ MeV} \end{equation}$$ $$\begin{equation} {}^2\text{H} + {}^3\text{H} \longrightarrow {}^4\text{He} + n + 17.6 \text{ MeV} \end{equation}$$

3. 受控热核反应：Lawson 判据

   $$\begin{equation} E_{in} \le E_{out} \end{equation}$$ $$\begin{equation} 3n k_B T + P_b \tau \le P_R \tau \end{equation}$$

附录

$$\frac{e^2}{4 \pi \varepsilon_0} = 1.44 \text{ fm} \cdot \text{MeV} = 1.44 \text{ nm} \cdot \text{eV}$$ $$\hbar c = 197 \text{ fm} \cdot \text{MeV} = 197 \text{ nm} \cdot \text{eV}$$ $$hc = 1240 \text{ fm} \cdot \text{MeV} = 1240 \text{ nm} \cdot \text{eV}$$ $$m_p = 938 \text{ MeV}/c^2$$ $$m_n = 940 \text{ MeV}/c^2$$ $$m_e = 0.511 \text{ MeV}/c^2$$ $$1 \text{ u} = 931.5 \text{ MeV}/c^2 = 1.66 \times 10^{-27} \text{ kg}$$ $$\mu_B = 0.5788 \times 10^{-4} \text{ eV} \cdot \text{T}^{-1} = 0.927 \times 10^{-23} \text{ J} \cdot \text{T}^{-1}$$