多电子原子

中心力场近似

1. 第 $ i $ 个电子的总势能函数：原子核势场 + 其他电子的平均中心势场

   $$\begin{equation} V_i(r_i) = -\frac{Z e^2}{4 \pi \varepsilon_0 r_i} + V_{ai}(r_i) \end{equation}$$

2. 原子体系的零级近似 Hamilton 算符:

   $$\begin{equation} \hat{H}_0 = \sum_{i=1}^N \left( -\frac{\hbar^2}{2 m_i} \nabla_i^2 + V_i(r_i) \right) \end{equation}$$

3. 每个电子的定态 Schrodinger 方程:

   $$\begin{equation} \left[ -\frac{\hbar^2}{2 m} \nabla_i^2 + V_i(r_i) \right] \psi_i(r_i, \theta_i, \varphi_i) = \varepsilon_i \psi_i(r_i, \theta_i, \varphi_i), \quad i = 1, 2, \ldots, N \end{equation}$$ $$\begin{equation} \psi_{n_i l_i m_i}(r_i, \theta_i, \varphi_i) = R_{n_i l_i}(r_i) Y_{l_i m_i}(\theta_i, \varphi_i) \end{equation}$$

4. 第 $ i $ 个电子的量子态:

   $$\begin{equation} \phi_{n_i l_i m_i m_{s_i}} = \psi_{n_i l_i m_i}(r_i, \theta_i, \varphi_i) \chi_{m_{s_i}}(s_z) \end{equation}$$

其本征能量对$l$的兼并已解除，用$\epsilon_{n_i l_i} $表示

Pauli 不相容原理

1. Bose 子：自旋量子数为整数的粒子，波函数为交换对称，如光子、𝜋 介子。

   $$\begin{equation} \psi_s(1, 2) = \frac{1}{\sqrt{2}} [\psi_\alpha(1) \psi_\beta(2) + \psi_\alpha(2) \psi_\beta(1)] \end{equation}$$

2. Fermi 子：自旋量子数为半整数的粒子，波函数为交换反对称的，如电子、质子、中子等。

   $$\begin{equation} \psi_a(1, 2) = \frac{1}{\sqrt{2}} [\psi_\alpha(1) \psi_\beta(2) - \psi_\alpha(2) \psi_\beta(1)] \end{equation}$$

3. Pauli 不相容原理：任何两个 Fermi 子都不可能具有四个完全相同的量子数 $ n, l, m, m_s $。

原子的壳层结构

1. 原子的电子组态:

   $$\begin{equation} n_i l_i^{N_i} \end{equation}$$

2. 原子中电子的壳层结构:
   (1) 主壳层:

   1 2	n = 1 2 3 4 5 6 7 K L M N O P Q

   (2) 支壳层:

   1 2	l = 0 1 2 3 4 5 ... s p d f g h ...

3. 各壳层能容纳的电子数:
   (1) 主壳层 ($ n $ 相同):

   $$\begin{equation} N(n, l) = \sum_{l=0}^{n-1} 2(l + 1) = 2n^2 \end{equation}$$

   (2) 支壳层 ($ n, l $ 相同):

   $$\begin{equation} N(l) = 2(2l + 1) \end{equation}$$

4. 闭合壳层的特点

(1) 闭合支壳层的电子概率密度分布是球对称的。
(2) 闭合主壳层和支壳层的电子总角动量和磁矩均为 0。

闭合壳层的这两个特点，将大大简化对多电子原子能级的计算. 首先，闭合壳层内的电子对价电子的静电相互作用，可基本上看作是一种中心力场的作用，闭合壳层只起了屏蔽原子核的作用. 另外，价电子与闭合壳层内电子之间的磁相互作用等于零. 考虑原子的磁矩时，也只需计及价电子的磁矩.

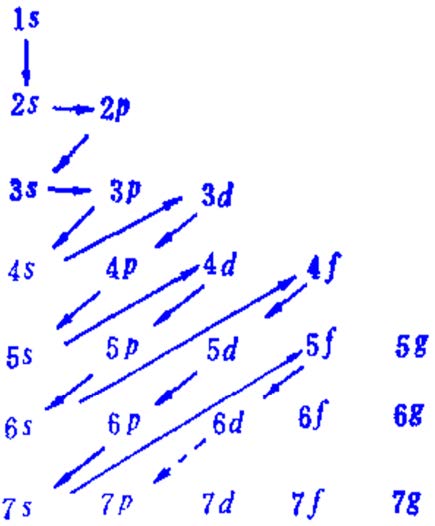
1. 支壳层的能量次序（经验公式）

$$\begin{equation} n + 0.7l \end{equation}$$

多电子原子能级的精细结构

剩余非中心库仑相互作用和自旋—轨道相互作用

$n,l,m,m_s$或$n,l,j,m_j$都可完整描述原子中电子的运动状态。

1. 多电子原子的剩余非中心库仑相互作用修正：

   $$\begin{equation} \hat{H}_1 = \sum_{i=1, j=1, i \neq j}^N \frac{1}{2} \frac{e^2}{4 \pi \varepsilon_0 r_{ij}} - \sum_{i=1}^N V_{ai}(r_i) \end{equation}$$

2. 电子的自旋-轨道相互作用修正：

   $$\begin{equation} \hat{H}_2 = \sum_{i=1}^N \frac{\mu_0 Z^* e^2}{8 \pi m_e^2 r_i^3} s_i \cdot \ell_i \end{equation}$$

$\mathcal{LS}$ 耦合

对应原子中电子自身的自旋—轨道相互作用小于非中心剩余库仑相互作用，故先考虑后者。

原子总轨道角动量$\boldsymbol{L}$守恒（$\boldsymbol{L}^2$有确定本征值 ），在量子力学中量子数$L$是表征原子态的好量子数.

$LS$耦合情况对应的$\boldsymbol{L}^2$，$\boldsymbol{S}^2$，$\boldsymbol{J}^2$和$J_z$是守恒量，它们相互对易，同时具有确定值。这时，描述原子状态的好量子数为$L$，$S$，$J$和$M_J$四个量子数。

1. 原子的总轨道角动量：

   $$\begin{equation} \mathcal{L} = \ell_1 + \ell_2 \end{equation}$$ $$\begin{equation} \mathcal{L} = \sqrt{L(L + 1)} \hbar^2, \quad L = |l_1 - l_2|, \ldots, l_1 + l_2 \end{equation}$$ $$\begin{equation} \mathcal{L}_z = M_L \hbar, \quad M_L = 0, \pm 1, \ldots, \pm L \end{equation}$$

2. 原子的总自旋角动量：

   $$\begin{equation} \mathcal{S} = s_1 + s_2 \end{equation}$$ $$\begin{equation} \mathcal{S} = \sqrt{S(S + 1)} \hbar^2, \quad S = |s_1 - s_2|, \ldots, s_1 + s_2 \end{equation}$$ $$\begin{equation} \mathcal{S}_z = M_S \hbar, \quad M_S = 0, \pm 1, \ldots, \pm S \end{equation}$$

3. 原子的总角动量：

   $$\begin{equation} \mathcal{J} = \mathcal{L} + \mathcal{S} \end{equation}$$ $$\begin{equation} \mathcal{J} = \sqrt{J(J + 1)} \hbar, \quad J = |L - S|, \ldots, L + S \end{equation}$$ $$\begin{equation} \mathcal{J}_z = M_J \hbar, \quad M_J = 0, \pm 1, \ldots, \pm J \end{equation}$$

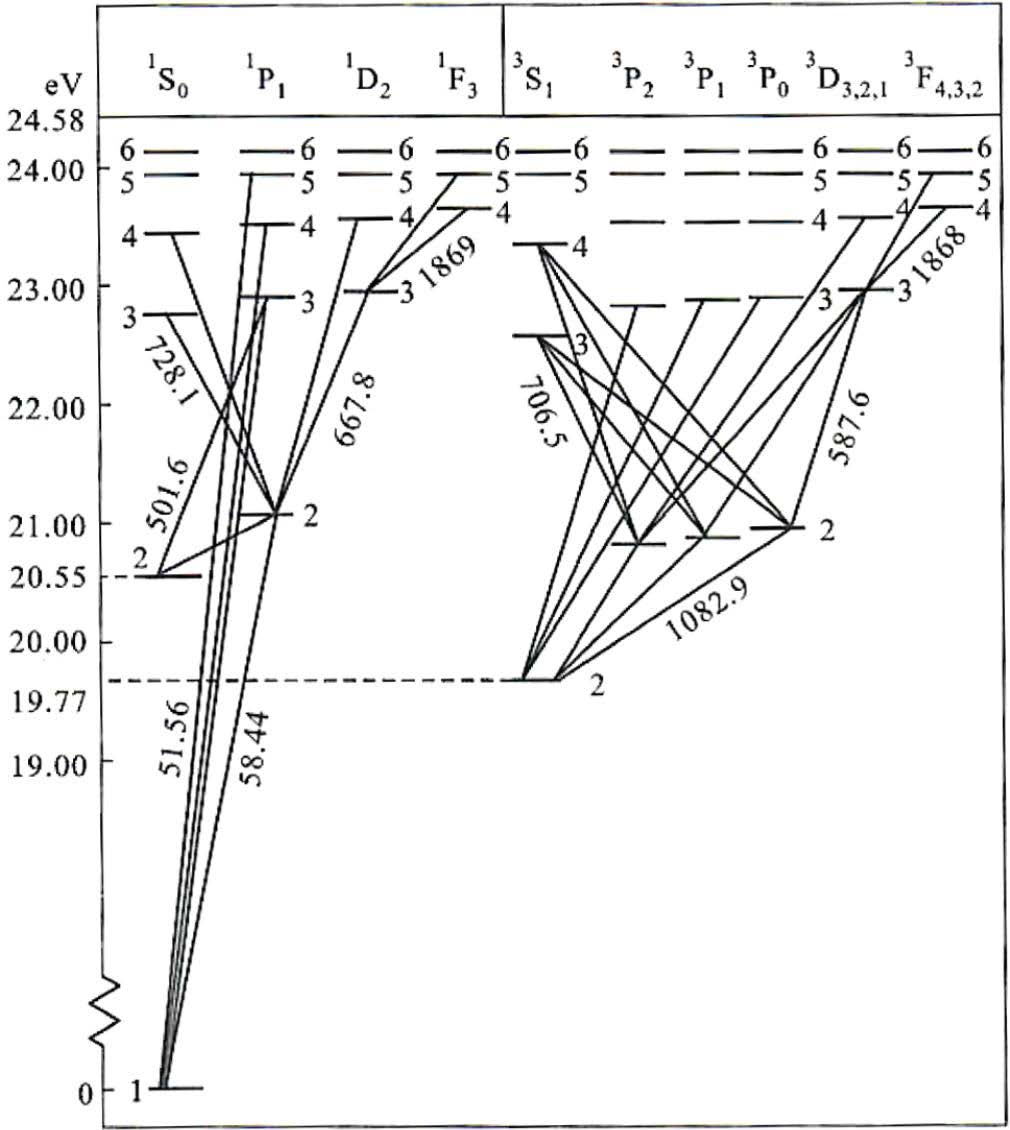
4. 每个精细结构能级由 $L$、$S$、$J$ 值表示。在电子组态给定后，整个原子的状态称为原子态，用这三个量子数标志，光谱学中通常用符号$^{2S + 1}L_J$表示。

5. 电子的自旋-轨道耦合修正:

$$\begin{equation} \Delta E_{LS} = \frac{1}{2} A(L, S) [J(J + 1) - L(L + 1) - S(S + 1)] \hbar^2 \end{equation}$$

1. Lande 间隔定则(即对同一多重态，两个相邻能级间隔之比等于它们中较大的两个𝐽 值比):

$$\begin{equation} E_{J+1} - E_J = A(L, S) (J + 1) \hbar^2 \end{equation}$$

1. 部分非等效电子组态和等效电子组态 $LS$ 耦合后构成的原子态:

1. $Hund$ 定则: 给定电子组态，精细结构能级高低的顺序如下决定:

(1) 首先看 $S$ 值，$S$ 值较大的能级较低。

(2) 其次看 $L$ 值，$L$ 值较大的能级较低。

(3) （仅适用于同科电子）同一支壳层内，电子数小于等于闭合壳层容纳数的一半时，$J$ 值较小的能量较低，称为正序；电子数大于闭合壳层容纳数的一半时，$J$ 值较大的能量较低，称为倒序。

$\textbf{Remark}$: 对原子的一些激发组态，$\mathcal{LS}$ 耦合并不严格成立。但是，可以利用 Hund 定则确定原子基态。

$jj$ 耦合

对应原子中电子自身的自旋—轨道相互作用大于非中心剩余库仑相互作用。

分裂后的能级由 $j_1$、$j_2$ 和 $J$ 表示，标记为 $(j_1, j_2)_J$。在量子力学中，在 $jj$ 耦合近似下，力学量 $\boldsymbol{j}_1^2$、$\boldsymbol{j}_2^2$、$\boldsymbol{J}^2$ 和 $\boldsymbol{J}_z$ 是守恒量，且相互对易，同时具有确定值。

1. 电子的总角动量:

$$\begin{equation} j_i = \ell_i + s_i \end{equation}$$ $$\begin{equation} j_i = \sqrt{j(j + 1)} \hbar^2, \quad j_i = |l_i - s_i|, \ldots, l_i + s_i \end{equation}$$

1. 原子的总角动量:

$$\begin{equation} \mathcal{J} = j_1 + j_2 \end{equation}$$ $$\begin{equation} \mathcal{J} = \sqrt{J(J + 1)} \hbar^2, \quad J = |j_1 - j_2|, \ldots, j_1 + j_2 \end{equation}$$

多电子原子的光谱

电偶极辐射跃迁的选择定则

1. 电子组态的选择定则:

   $$\begin{equation} \Delta \left( \sum_i l_i \right) = \pm 1 \end{equation}$$

   在单电子跃迁情形下,

   $$\begin{equation} \Delta l = \pm 1 \end{equation}$$

2. 原子中相互作用的量子数选择定则:
   (1) $ \mathcal{LS} $ 耦合:

   $$\begin{equation} \begin{cases} \Delta S = 0 \\ \Delta L = 0, \pm 1\\ \Delta J = 0, \pm 1 \quad (J = 0 \rightarrow J = 0 \text{ 除外}) \\ \Delta M_J = 0, \pm 1 \end{cases} \end{equation}$$

   (2) $ jj $ 耦合:

   $$\begin{equation} \begin{cases} \Delta j_1 = 0 & \text{or} & \Delta j_1 = 0, \pm 1 \\ \Delta j_2 = 0, \pm 1 & & \Delta j_2 = 0 \\ \Delta J = 0, \pm 1 \quad (J = 0 \rightarrow J = 0 \text{ 除外}) \\ \Delta M_J = 0, \pm 1 \end{cases} \end{equation}$$

   $\textbf{Remark}$: 对总角动量量子数$J$的选择定则严格成立，但重原子 $ \mathcal{LS} $ 耦合中对 $ \Delta S = 0 $ 的选择定则并非严格成立。

氮原子的光谱

激光

Einstein 辐射理论

1. 自发辐射:

   $$\begin{equation} \left( \frac{\mathrm{d}N_2}{\mathrm{d}t} \right)_{\text{自发}} = -A_{21} N_2 \end{equation}$$

   (1) $ E_2 $ 能级上的原子数密度:

   $$\begin{equation} N_2 = N_{20} e^{-A_{21} t} = N_{20} e^{-t / \tau_2} \end{equation}$$

   (2) 一般说来，处于激发能级 $E{n}$ 的原子会自发跃迁到所有可能的低能级，能级 $E{n}$ 的平均寿命为

   $$\begin{equation} \tau_{n}=\frac{1}{\sum_{m}A_{nm}} \end{equation}$$

   (3) 谱线的自然宽度:

   $$\begin{equation} \Delta \nu = (\Delta E_n + \Delta E_m) / h \geqslant \frac{1}{4 \pi} \left( \frac{1}{\tau_n} + \frac{1}{\tau_m} \right) \end{equation}$$

   当 $ E_m $ 为基态能级时，$ \tau_m \rightarrow \infty $

   $$\begin{equation} \Delta \nu \geqslant \frac{1}{4 \pi \tau_n} \end{equation}$$

2. 受激辐射:

   $$\begin{equation} \left( \frac{\mathrm{d}N_2}{\mathrm{d}t} \right)_{\text{受激}} = -\rho(\nu) B_{21} N_2 \end{equation}$$

   受激发射的光子与入射光子在传播方向、频率、相位和偏振方向上完全相同，受激辐射使入射光得到相干放大，是相干光

3. 受激吸收:

   $$\begin{equation} \left( \frac{\mathrm{d}N_1}{\mathrm{d}t} \right)_{\text{受激}} = -\rho(\nu) B_{12} N_1 \end{equation}$$

4. Einstein 关系:
   (1) 热平衡下能级之间粒子数交换平衡:

   $$\begin{equation} \left( \frac{\mathrm{d}N_{12}}{\mathrm{d}t} \right)_{\text{受激}} = \left( \frac{\mathrm{d}N_{21}}{\mathrm{d}t} \right)_{\text{自发}} + \left( \frac{\mathrm{d}N_{21}}{\mathrm{d}t} \right)_{\text{受激}} \end{equation}$$

   (2) 热平衡下两能级上原子数密度之比服从 Boltzmann 分布:

   $$\begin{equation} \frac{N_2}{N_1} = \frac{g_1}{g_2} \exp \left( -\frac{E_2 - E_1}{k_B T} \right) \end{equation}$$

   (3) 解出入射谱能量密度:

   $$\begin{equation} \rho(\nu) = \frac{A_{21}}{\frac{g_1}{g_2} B_{12} \exp \left( h \nu / k_B T \right) - B_{21}} \end{equation}$$

   (4) 在高温极限下: $ k_B T \gg E_2 - E_1 = h \nu $

   $$\begin{equation} \rho(\nu) = \frac{A_{21}}{\left( \frac{g_1}{g_2} B_{12} - B_{21} \right) + B_{12} h \nu / k_B T} \end{equation}$$

   (5) 对比Rayleigh-Kings公式，得$ A, B $ 系数的 Einstein 关系:

   $$\begin{equation} B_{12} = \frac{g_1}{g_2} B_{21}, \quad \frac{A_{21}}{B_{21}} = \frac{8 \pi h \nu^3}{c^3} \end{equation}$$

激光原理

1. 激光器的结构: 激励能源、激活介质、光学共振腔。

2. 激光器的分类: 固体激光器、气体激光器、半导体激光器、染料激光器、自由电子激光器。

3. 产生激光的必要条件:
   (1) 受激辐射大于受激吸收: 粒子数反转, $ N_2 > N_1 $（激活介质、激励能源、抽运过程）

   (2) 受激辐射大于自发辐射:

   $$\begin{equation} B_{21} \rho(\nu) > A_{21} \end{equation}$$

   (3) 阈值条件: 外界激励功率超过损耗阈值

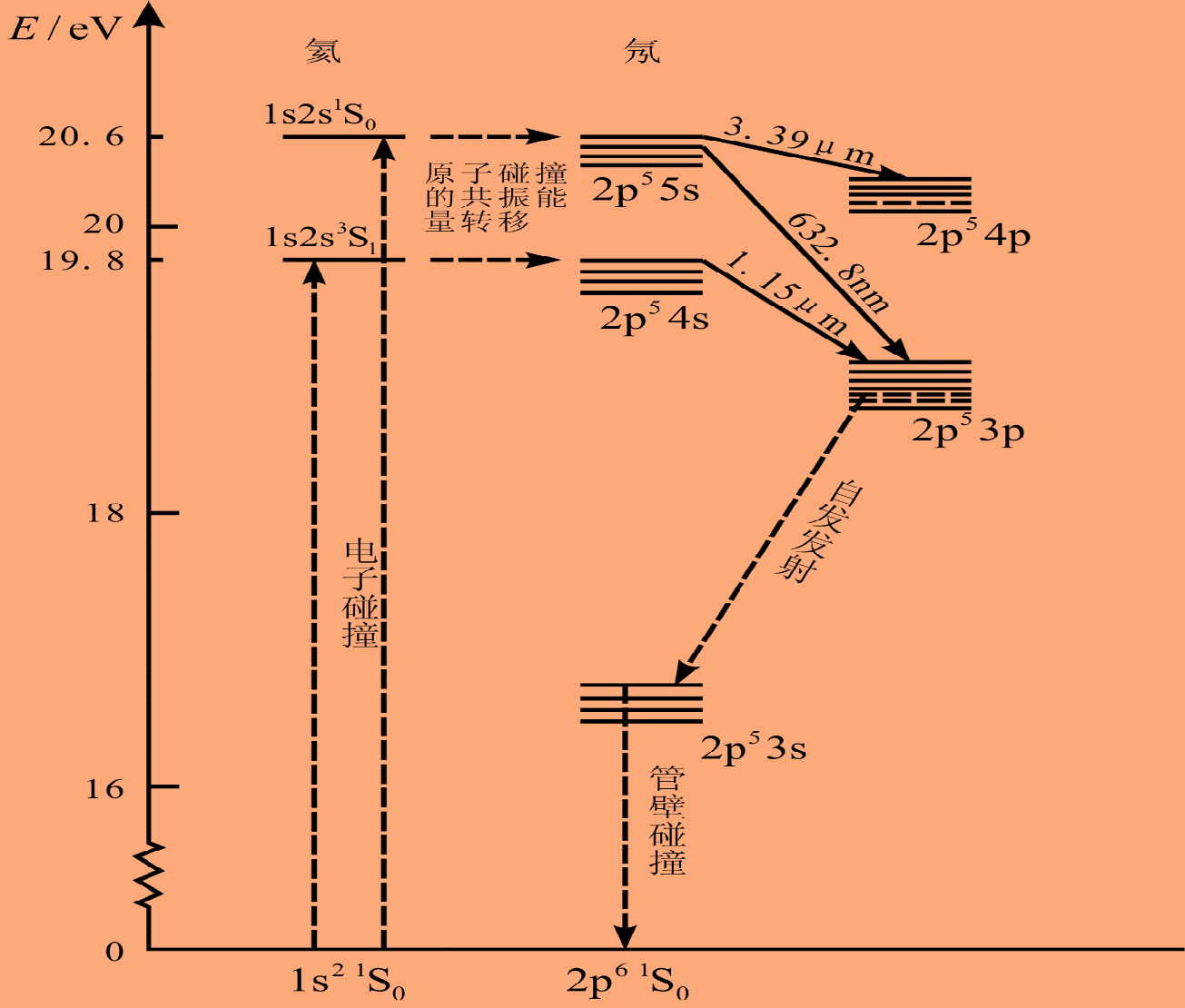
4. He-Ne激光器

• 工作物质： 氖气

• 激励方式：直流气体放电

电子经电场加速后，与$\mathrm{He}$碰撞。处于激发态的$\mathrm{He}$与$\mathrm{Ne}$碰撞，把能量传递给$\mathrm{Ne}$，使它在亚稳态$(2p^{5}5s$、$2p^{5}4s$ ）和激发态（$2p^{5}4p$、$2p^{5}3p$ ）之间形成反转分布。

1. 红宝石激光器

• 激励能源：脉冲氙灯
• 工作物质：红宝石中的$\mathrm{Cr}^{+3}$

脉冲氙灯发出的光照射红宝石，使得$\mathrm{Cr}^{+3}$在亚稳态和基态之间形成反转分布。

X 射线

X 射线的产生机制

1. X 射线谱:
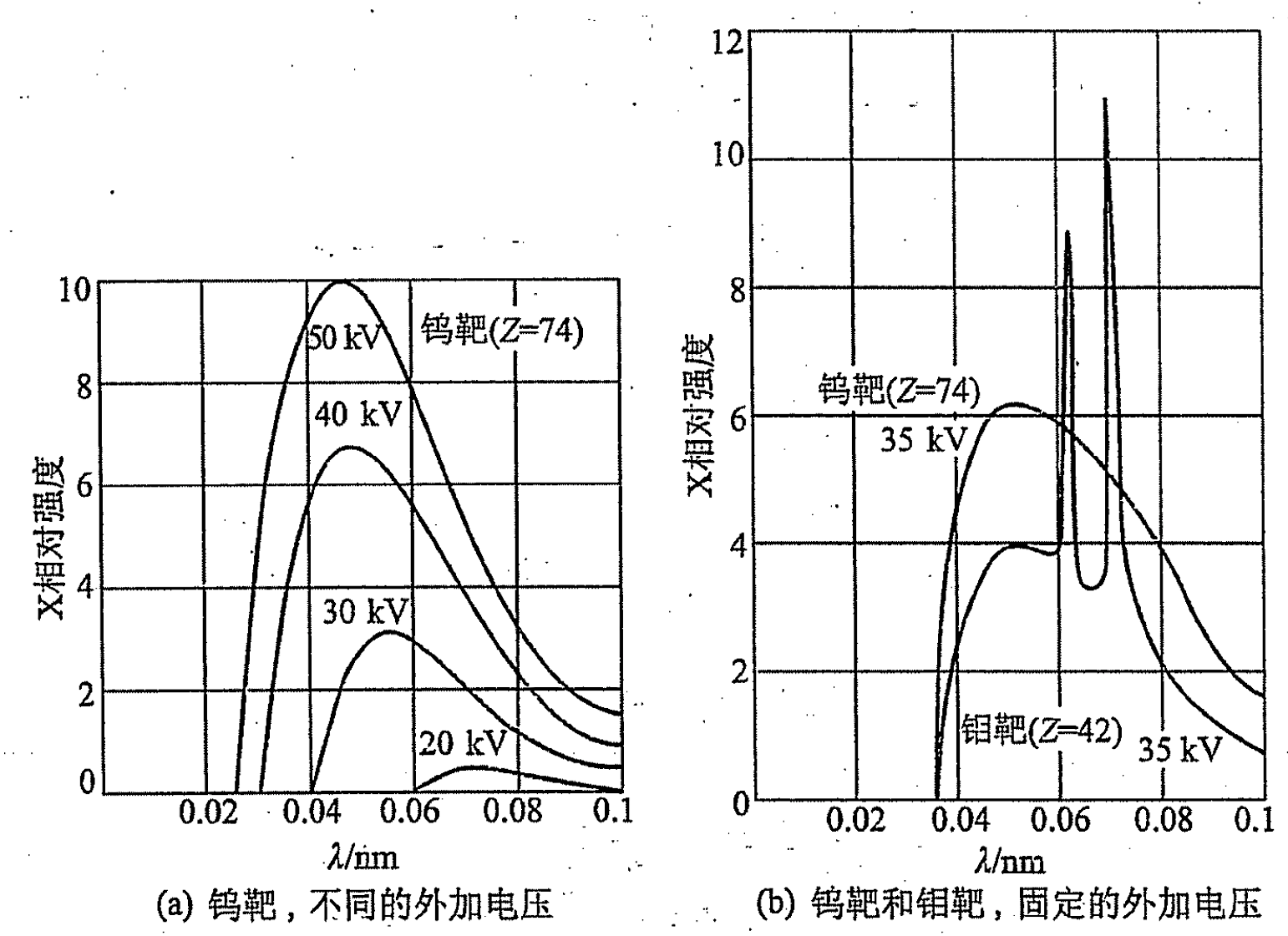
   (1) X 射线的连续谱：带电粒子与原子（原子核）相碰撞，发生骤然减速时，动能->辐射能，由此伴随产生的辐射为轫致射辐。
   存在最小波长(电子在电场中得到的动能全部转成辐射能，一个电子仅辐射一个光子时)：

   $$\begin{equation} \lambda_\text{最小}=\frac{c}{\nu}=\frac{hc}{h\nu}=\frac{hc}{eV}=\frac{1.24}{V(\mathrm{kV})}\mathrm{nm} \end{equation}$$

   (2) X 射线的特征谱：内壳层电子跃迁。

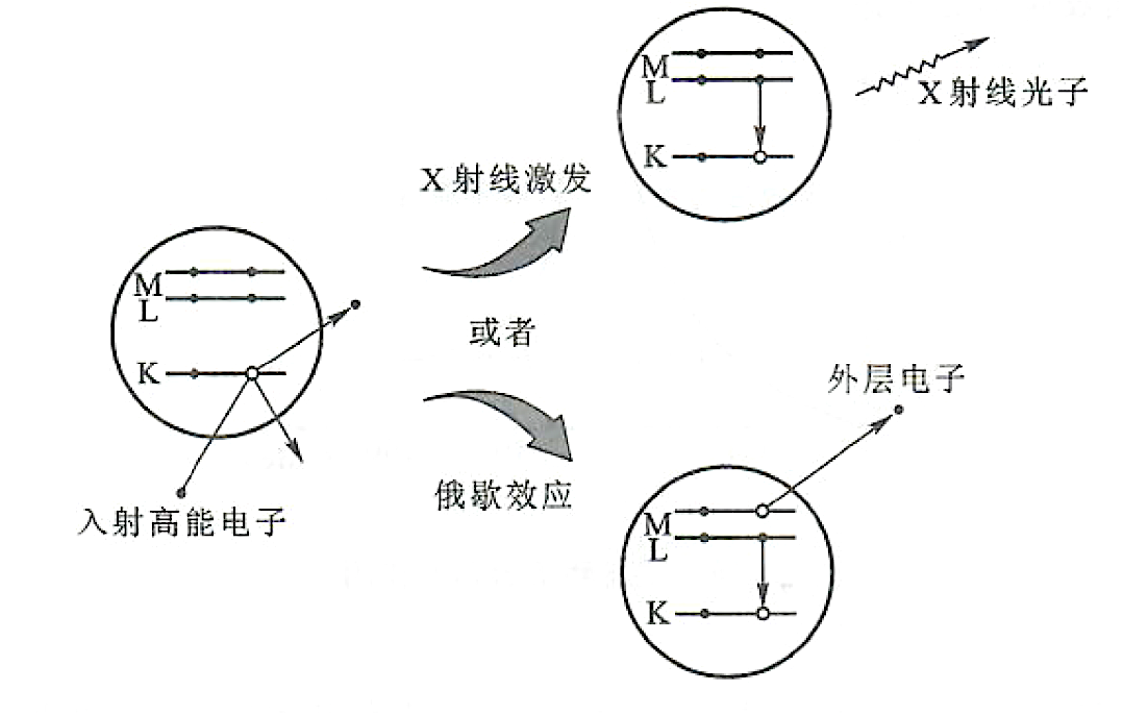
   在外界作用下，如一个能量足够高的入射电子碰撞原子，使原子的内壳层电子电离，在内壳层产生了一个空位，外壳层电子将跃迁至这个空位，并发射一个光子，由于内壳层电子的束缚能比外壳层电子大得多，发射的光子频率一般落在X 射线波段，这样形成了X 射线的特征发射谱. 内壳层电子也可以吸收外来的X 射线光子而被电离，这就形成了X 射线的特征吸收谱.

1. Moseley 定律:

   若是一个L 电子被电离，留下一个空位，填充电子来自M、N、O 等壳层，发出的 X 射线相应地称为 L𝛼、L𝛽、L𝛾，等线，依此类推.

   $$\begin{equation} \tilde{\nu}_{K_\alpha} = R(Z - 1)^2 \left( \frac{1}{1^2} - \frac{1}{2^2} \right) \end{equation}$$ $$\begin{equation} \tilde{\nu}_{L_\alpha} = R(Z - 7.4)^2 \left( \frac{1}{2^2} - \frac{1}{3^2} \right) \end{equation}$$

2. 俄歇效应:

   当原子内壳层出现空位，较外层电子跃迁至这个空位时，其多余的能量不一定通过发射X 射线释放，也可能将多余的能量通过库仑相互作用传给另一个外层电子，使其电离，这是一种非辐射退激发过程.

   

   $$\begin{equation} E = E_K - E_L - E_M \end{equation}$$

X 射线的吸收*

1. Lambert-Beer 定律:

   $$\begin{equation} I = I_0 e^{-\alpha x} = I_0 e^{-\mu \rho x} \end{equation}$$

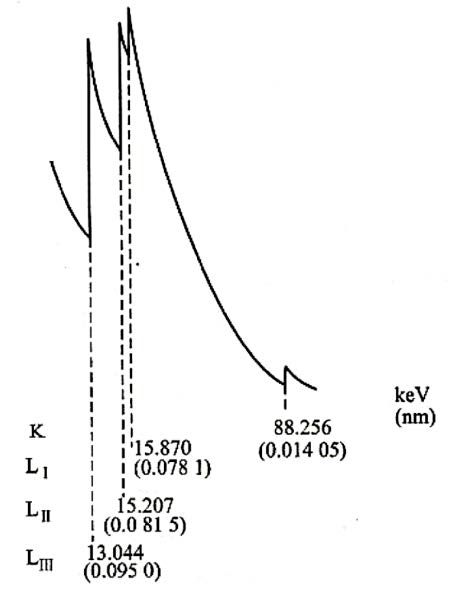
2. 低能 X 射线的质量吸收系数:

   $$\begin{equation} \mu = \mu_{\text{光电}} + \mu_{\text{compton}} + \mu_{\text{rayleigh}} \end{equation}$$

3. 吸收限: X 射线使一个内壳层电子脱离原子

1. 扩展 X 射线吸收的精细结构: 被打出电子的波被周围原子散射形成向内的波，与原来向外的波干涉