氢原子与碱金属原子

氢原子

氢原子的定态 Schrodinger 方程

1. 定态 Schrodinger 方程: $$\begin{equation} -\frac{\hbar^2}{2\mu} \nabla^2 \psi(r, \theta, \varphi) - \frac{e^2}{4\pi\varepsilon_0 r} \psi(r, \theta, \varphi) = E \psi(r, \theta, \varphi) \end{equation}$$
2. Laplace 算子: $$\begin{equation} \nabla^2 = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial}{\partial r} \right) + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} \right) + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2}{\partial \varphi^2} \end{equation}$$
3. 分离变量: $$\begin{equation} \psi(r, \theta, \varphi) = R(r) \Theta(\theta) \Phi(\varphi) \end{equation}$$

$$\begin{equation} \frac{\sin^2 \theta}{R} \frac{\mathrm{d}}{\mathrm{d}r} \left( r^2 \frac{\mathrm{d}R}{\mathrm{d}r} \right) + \frac{\sin \theta}{\Theta} \frac{\mathrm{d}}{\mathrm{d}\theta} \left( \sin \theta \frac{\mathrm{d}\Theta}{\mathrm{d}\theta} \right) + \frac{2\mu r^2}{\hbar^2} \sin^2 \theta \left( E + \frac{e^2}{4\pi\varepsilon_0 r} \right) = -\frac{1}{\Phi} \frac{\mathrm{d}^2 \Phi}{\mathrm{d}\varphi^2} = m^2 \end{equation}$$ $$\begin{equation} \frac{1}{R} \frac{\mathrm{d}}{\mathrm{d}r} \left( r^2 \frac{\mathrm{d}R}{\mathrm{d}r} \right) + \frac{2\mu r^2}{\hbar^2} \left( E + \frac{e^2}{4\pi\varepsilon_0 r} \right) = \frac{m^2}{\sin^2 \theta} - \frac{1}{\Theta \sin \theta} \frac{\mathrm{d}}{\mathrm{d}\theta} \left( \sin \theta \frac{\mathrm{d}\Theta}{\mathrm{d}\theta} \right) = l(l+1) \end{equation}$$

1. 方位角部分: $$\begin{equation} \frac{\mathrm{d}^2 \Phi}{\mathrm{d}\varphi^2} + m^2 \Phi = 0 \end{equation}$$

$$\begin{equation} \Phi_m(\varphi) = \frac{1}{\sqrt{2\pi}} e^{im\varphi}, \quad m = 0, \pm 1, \pm 2, \ldots, \pm l \end{equation}$$

1. 极角部分: $$\begin{equation} \frac{1}{\sin \theta} \frac{\mathrm{d}}{\mathrm{d}\theta} \left( \sin \theta \frac{\mathrm{d}\Theta}{\mathrm{d}\theta} \right) \Theta + \left[ l(l+1) - \frac{m^2}{\sin^2 \theta} \right] \Theta = 0 \end{equation}$$

$$\begin{equation} \Theta_{lm}(\theta) = A P_l^m(\cos \theta), \quad l = 0, 1, 2, \ldots, n-1 \end{equation}$$

1. 径向部分: $$\begin{equation} \left( \frac{\mathrm{d}^2}{\mathrm{d}r^2} + \frac{2}{r} \frac{\mathrm{d}}{\mathrm{d}r} \right) R + \left[ \frac{2\mu}{\hbar^2} \left( E + \frac{e^2}{4\pi\varepsilon_0 r} \right) - \frac{l(l+1)}{r^2} \right] R = 0 \end{equation}$$

$$\begin{equation} R_{nl} = N_{nl} e^{-Zr/na} \left( \frac{2Zr}{na} \right)^l L_{n+1}^{2l+1} \left( \frac{2Zr}{na} \right), \quad N_{nl} = -\sqrt{\left( \frac{2Z}{na} \right)^3 \frac{(n-l-1)!}{2n[(n+1)!]^3}} \end{equation}$$

1. 波函数: $$\begin{equation} \psi_{nlm}(r, \theta, \varphi) = R_{nl}(r) \Theta_{lm}(\theta) \Phi_m(\varphi) = R_{nl}(r) Y_l^m(\theta, \varphi) \end{equation}$$

$$\begin{equation} \psi_{1,0,0}(r, \theta, \varphi) = \frac{1}{\sqrt{\pi a^3}} e^{-r/a} \end{equation}$$

三个量子数的物理意义

1. 主量子数 $ n $ 和能级:
   (1) $\hat{H}$ 的本征方程:

   $$\begin{equation} \hat{H} \psi_{nlm}(r, \theta, \varphi) = E_n \psi(r, \theta, \varphi) \end{equation}$$

   (2) 能级:

   $$\begin{equation} E_n = -\left[ \frac{\mu}{2\hbar^2} \left( \frac{Ze^2}{4\pi\varepsilon_0} \right)^2 \right] \frac{1}{n^2} = -\frac{Rhc}{n^2} = \frac{E_1}{n^2}, \quad n = 1, 2, \ldots \end{equation}$$

   (3) 能级的简并度(同一能级，氢原子有$n^2$个本征态):

   $$\begin{equation} N(n, l, m) = \sum_{l=0}^{n-1} (2l+1) = \frac{n(1+2n-1)}{2} = n^2 \end{equation}$$

2. 角量子数 $ l $ 和轨道角动量:
   (1) $\hat{L}^2$ 的本征方程:

   $$\begin{equation} \hat{L}^2 Y_l^m(\theta, \varphi) = l(l + 1) \hbar^2 Y_l^m(\theta, \varphi) \end{equation}$$

   (2) 轨道角动量的大小:

   $$\begin{equation} L = \sqrt{l(l + 1)} \hbar, \quad l = 0, 1, 2, \ldots, n - 1 \end{equation}$$

3. 磁量子数 $ m $ 和轨道角动量空间取向:
   (1) $\hat{L}_z$ 的本征方程:

   $$\begin{equation} \hat{L}_z Y_l^m(\theta, \varphi) = m \hbar Y_l^m(\theta, \varphi) \end{equation}$$

   (2) 轨道角动量 $ z $ 分量的大小:

   $$\begin{equation} L_z = m \hbar, \quad m = 0, \pm 1, \pm 2, \ldots, \pm l \end{equation}$$

电子概率密度分布

1. 空间概率分布:

   $$\begin{equation} |\psi_{nlm}(r, \theta, \varphi)|^2 |d\tau| = |R_{nl}(r)|^2 |Y_l^m(\theta, \varphi)|^2\boldsymbol{ r^2 \sin \theta} dr d\theta d\varphi \end{equation}$$

2. 角向概率分布:

   $$\begin{equation} P_{lm}(\theta, \varphi) d\Omega = \int_0^{+\infty} |R_{nl}(r)|^2 r^2 dr |Y_l^m(\theta, \varphi)|^2 \boldsymbol{ \sin \theta }d\theta d\varphi = |Y_l^m(\theta, \varphi)|^2 d\Omega \end{equation}$$

3. 径向概率分布:

   $$\begin{equation} P_{nl}(r) dr = \int_0^{2\pi} d\varphi \int_0^\pi |Y_l^m(\theta, \varphi)|^2 \sin \theta d\theta |R_{nl}(r)|^2 r^2 dr = R_{nl}^2(r) r^2 dr \end{equation}$$

   $P_{nl}(r)$ 有 $ n - l $ 个极大值点，$ n - l - 1 $ 个极小值点。主峰位置随 $ l $ 增加向原子核移近。$ l $ 值越小，最内层的峰离核越近，说明对同一 $ n $ 值，随着 $ l $ 的减小，电子出现在原子核附近的概率逐渐增大。

4. 电子径向坐标的平均值:

   $$\begin{equation} \langle r \rangle = \frac{1}{2} [3n^2 - l(l + 1)] \frac{a_1}{Z} \end{equation}$$ $$\begin{equation} \langle r^2 \rangle = \frac{1}{2} [5n^2 + 1 - l(l + 1)] n^2 \left( \frac{a_1}{Z} \right)^2 \end{equation}$$ $$\begin{equation} \langle r^{-1} \rangle = \frac{Z}{a_1 n^2} \end{equation}$$

定态的宇称

1. 空间反演算符:

   $$\begin{equation} \hat{P} \psi_{nlm}(r, \theta, \varphi) = \psi_{nlm}(r, \pi - \theta, \varphi + \pi) \end{equation}$$

2. 氢原子定态的宇称取决于 $ l $:

   $$\begin{equation} Y_l^m(\pi - \theta, \varphi + \pi) = (-1)^l Y_l^m(\theta, \varphi) \end{equation}$$ $$\begin{equation} \hat{P} \psi_{nlm}(r, \theta, \varphi) = (-1)^l \psi_{nlm}(r, \theta, \varphi) \end{equation}$$

跃迁的选择定则

1. 感生偶极矩算符:

   $$\begin{equation} \hat{D} = -e r \end{equation}$$

2. 电偶极跃迁矩阵元:

   $$\begin{equation} D_{nn'} = \int_{-\infty}^{+\infty} \psi_n^*(r) \hat{D} \psi_{n'}(r) d\tau \end{equation}$$

   在 $ \psin(r) $ 和 $ \psi{n’}(r) $ 间发生跃迁的概率正比于 $ |D_{nn’}|^2 $。

3. 发生电偶极辐射跃迁的条件

$$\begin{equation} \langle e r_{ij} \rangle = e \langle j | r | i \rangle = e \int_{-\infty}^{+\infty} \psi_{n_2 l_2 m_2}^* r \psi_{n_1 l_1 m_1} \neq 0 \end{equation}$$

(1) 方位角部分:

$$\begin{equation} x: \int_0^{2\pi} \left[ e^{i(m_1 - m_2 + 1)\varphi} + e^{i(m_1 - m_2 - 1)\varphi} \right] d\varphi \end{equation}$$ $$\begin{equation} y: \int_0^{2\pi} \left[ e^{i(m_1 - m_2 + 1)\varphi} - e^{i(m_1 - m_2 - 1)\varphi} \right] d\varphi \end{equation}$$ $$\begin{equation} z: \int_0^{2\pi} e^{i(m_1 - m_2)\varphi} d\varphi \end{equation}$$

磁量子数的选择定则:

$$\Delta m = m_2 - m_1 = 0, \pm 1$$

(2) 极角部分:

$$\begin{equation} \int_0^\pi \Theta_{l_2 m_2}^* \cos \theta \Theta_{l_1 m_1} \sin \theta d\theta = \int_0^\pi \Theta_{l_2 m_2}^* \frac{(l_1 - m_1 + 1) \Theta_{l_1 + 1, m_1} + (l_1 + m_1) \Theta_{l_1 - 1, m_1}}{2 l_1 + 1} \sin \theta d\theta \end{equation}$$ $$\begin{equation} \int_0^\pi \Theta_{l_2, m_2}^* \sin \theta \Theta_{l_1, m_1} \sin \theta d\theta = \int_0^\pi \Theta_{l_2, m_2}^* \frac{\Theta_{l_1 + 1, m_1} + \Theta_{l_1 - 1, m_1}}{2 l_1 + 1} \sin \theta d\theta \end{equation}$$

角量子数的选择定则 (Laporte 选择定则):

$$\Delta l = l_2 - l_1 = \pm 1$$

碱金属原子

1. 碱金属原子能级的粗结构:
   (1) 对同一主量子数 $ n $，碱金属能级位置低于氢原子。
   (2) 对同一主量子数 $ n $，不同角量子数 $ l $ 导致能级分裂。

2. 碱金属原子能级低于H的原因:
   (1) 原子实极化：价电子对原子实有极化作用。
   (2) 轨道贯穿：价电子有一定概率出现在原子实内。

   原子实的有效电荷数$𝑍^∗ > 1$，使得碱金属原子能量降低.(用量子力学的观点就是价电子的波函数在原子实内部不为零)

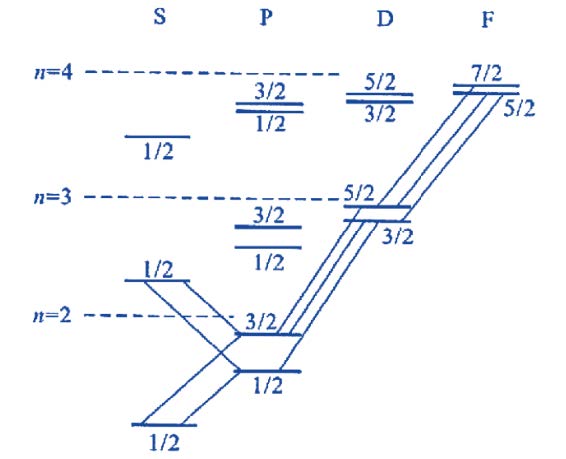
3. 碱金属原子的能级和光谱项:

   $$\begin{equation} E_{nl} = -\frac{RhcZ^{*2}}{n^2} = -\frac{Rhc}{n^{*2}} = -\frac{Rhc}{(n - \Delta_{nl})^2} \end{equation}$$ $$\begin{equation} T_{nl} = -\frac{E_{nl}}{hc} = \frac{R}{(n - \Delta_{nl})^2} \end{equation}$$

不同能级之间的跃迁遵守电偶极跃迁规则. 跃迁前后角量子数𝑙 的变化满足Δ𝑙 = ±1. 图中由𝑛𝑝 向2𝑠 跃迁的，即𝑛𝑝 → 2𝑠 为主线系，𝑛𝑠 → 2𝑝 为第二辅线系，𝑛𝑑 → 2𝑝为第一辅线系，𝑛𝑓 → 3𝑑 为柏格曼系. 2𝑝 向基态2𝑠 的跃迁产生的谱线称为共振线.

电子的自旋与磁矩

电子轨道的磁矩

1. 电子轨道的磁矩:

   $$\begin{equation} \boldsymbol{\mu_l} = -\frac{e}{2m_e} \boldsymbol{L} = -\gamma \boldsymbol{L} \end{equation}$$

2. 电子轨道的磁矩的大小:

   $$\begin{equation} \mu_l = -\sqrt{l(l + 1)} \frac{e\hbar}{2m_e} = -\sqrt{l(l + 1)} \mu_B \end{equation}$$

3. 电子轨道的磁矩 $ z $ 分量的大小:

   $$\begin{equation} \mu_{lz} = -m_z \frac{e\hbar}{2m_e} = -m \mu_B \end{equation}$$

Stern-Gerlach 实验

1. 作用于原子磁偶极矩上的力:

   $$\begin{equation} F_z = -\frac{\partial}{\partial z} (-\mu \cdot B) = \mu_z \frac{\mathrm{d}B}{\mathrm{d}z} \end{equation}$$

2. 横向位移:

   $$\begin{equation} s = \frac{1}{2} a t^2 = \frac{1}{2} \frac{F_z}{M_{Ag}} \left( \frac{d}{v} \right)^2 = \frac{1}{2 M_{Ag}} \frac{\mathrm{d}B}{\mathrm{d}z} \left( \frac{d}{v} \right)^2 \mu_z \end{equation}$$

电子自旋的磁矩

1. 电子自旋角动量量子数:

   $$\begin{equation} 2s + 1 = 2 \Rightarrow s = \frac{1}{2} \end{equation}$$

2. 电子自旋角动量:
   (1) 电子自旋角动量的大小:

   $$\begin{equation} |\boldsymbol{s}| = \sqrt{s(s + 1)} \hbar = \frac{\sqrt{3}}{2} \hbar \end{equation}$$

   (2) 电子自旋角动量 $ z $ 分量的大小:

   $$\begin{equation} s_z = m_s \hbar, \quad m_s = \pm \frac{1}{2} \end{equation}$$

3. 电子自旋的磁矩:
   (1) 电子自旋磁矩和自旋角动量的关系:

   $$\begin{equation} \boldsymbol{\mu_s} = -\frac{e}{m_e} \boldsymbol{S} \end{equation}$$

   (2) 电子自旋磁矩的大小:

   $$\begin{equation} \mu_s = \frac{e}{m_e} s = 2 \sqrt{s(s + 1)} \mu_B = \sqrt{3} \mu_B \end{equation}$$

4. 电子轨道和自旋磁矩的公式:

   $$\begin{equation} \mu_l = -g_l \frac{e}{2m_e} \ell, \quad g_l = 1 \end{equation}$$ $$\begin{equation} \mu_s = -g_s \frac{e}{2m_e} s, \quad g_s = 2 \end{equation}$$

5. 电子量子态的波函数:

   $$\begin{equation} \phi_{nlmm_s} = \psi_{nlm}(r, \theta, \varphi) \chi_{m_s}(s_z) \end{equation}$$

碱金属原子光谱的精细结构

原子的总角动量

1. 原子的总角动量:

   $$\begin{equation} \mathcal{J} = \mathcal{L} + \mathcal{S} \end{equation}$$

2. 总角动量的大小:

   $$\begin{equation} \mathcal{J} = \sqrt{J(J + 1)} \hbar, \quad J = |L - S|, \ldots, L + S \end{equation}$$

3. 总角动量 $ z $ 分量的大小:

   $$\begin{equation} \mathcal{J}_z = M_J \hbar, \quad M_J = 0, \pm 1, \ldots, \pm J \end{equation}$$

4. $\mathcal{LS}$ 耦合不改变碱金属原子量子态的数目:

   $$\begin{equation} N(n, l, m, m_s) = \sum_{l=0}^{n-1} 2(2l + 1) = 2n^2 \end{equation}$$ $$\begin{equation} N(n, l, j, m_j) = \sum_{l=0}^{n-1} \sum_{j=l-1/2}^{l+1/2} (2j + 1) = \sum_{l=0}^{n-1} 2(2l + 1) = 2n^2 \end{equation}$$

自旋-轨道相互作用

自旋 − 轨道耦合 使得 同一l能级进一步分裂为两个值 （能级精细结构）

j 值大的能级高， j 值小的能级低

s 态不分裂

1. 原子实在电子处产生的磁感应强度:

   $$\begin{equation} B = \frac{\mu_0}{4\pi} \frac{Z^* e v}{r^2} e_z = \frac{\mu_0}{4\pi} \frac{Z^* e}{m_e r^3} \ell \end{equation}$$

   在原子实静止系中，Thomas 给出右面应乘 1/2:

   $$\begin{equation} B = \frac{\mu_0}{8\pi} \frac{Z^* e}{m_e r^3} \ell \end{equation}$$

2. 自旋-轨道耦合能:

   $$\begin{equation} \Delta E_{ls} = -\mu_s \cdot B = \frac{\mu_0}{8\pi} \frac{Z^* e^2}{m_e^2 r^3} s \cdot \ell \end{equation}$$

3. 自旋-轨道耦合能在原子定态中的平均值:

   $$\begin{equation} \langle L \cdot S \rangle = \frac{1}{2} \langle J^2 - L^2 - S^2 \rangle = \frac{1}{2} [j(j + 1) - l(l + 1) - s(s + 1)] \hbar^2 \end{equation}$$ $$\begin{equation} \left\langle \frac{1}{r^3} \right\rangle = \frac{Z^{*3}}{n^3 l (l + 1/2) (l + 1) a^3} \end{equation}$$ $$\begin{equation} \Delta E_{ls} = \frac{R h c \alpha^2 Z^{*4}}{2 n^3} \frac{j(j + 1) - l(l + 1) - s(s + 1)}{l(l + 1/2)(l + 1)} \hbar^2 \end{equation}$$

碱金属原子光谱的精细结构

1. 碱金属原子总能量:

   $$\begin{equation} E_{nlj} = E_{nl} + \Delta E_{ls} \end{equation}$$

2. 双重能级:

   $$\begin{equation} j(j + 1) - l(l + 1) - s(s + 1) = \begin{cases} l & j = l + \frac{1}{2}, \quad l \neq 0 \\ -(l + 1) & j = l - \frac{1}{2} \end{cases} \end{equation}$$

3. 双重能级间隔:

   $$\begin{equation} \Delta E = \frac{R h c \alpha^2 Z^{*4}}{n^3 l (l + 1)} \end{equation}$$

4. 波数间隔:

   $$\begin{equation} \Delta \tilde{\nu} = \frac{R \alpha^2 Z^{*4}}{n^3 l (l + 1)} \end{equation}$$

5. 精细能级跃迁的选择定则:

   $$\begin{equation} \Delta J = 0, \pm 1, \quad \Delta l = \pm 1 \end{equation}$$

6. 原子能级符号:

   $$\begin{equation} n^{2S+1} L_J \end{equation}$$

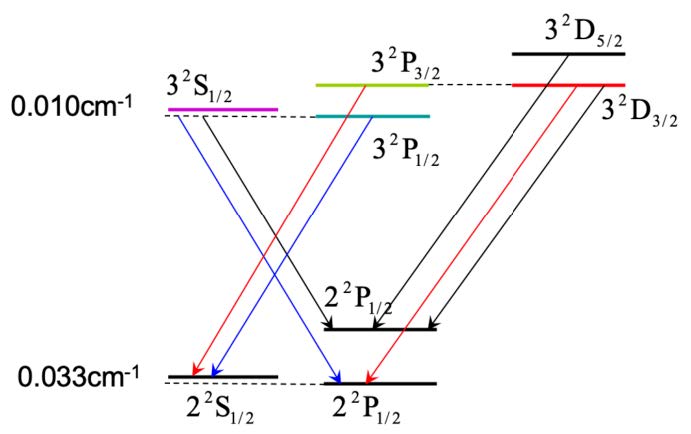
图 1: 锂原子能级能级的精细结构及允许跃迁

碱金属原子能级精细结构的几个特点：

1. 双重能级分裂的大小与有效核电荷数$𝑍^∗$ 的四次幂成正比，随着原子序数的增大，$𝑍^∗$ 也增大，所以高原子序数$Z$ 的原子双重能级分裂大.
2. $n^2 S_{1/2}$能级不存在精细分裂，因为$𝑙 = 0$ 时，不存在轨道运动产生的磁场，但通常
   仍保留多重数为2 的标记.S
   1. $Δ𝐸_{𝑙𝑠}$ 反比于$𝑛^3$ 和$𝑙^3$，对同一原子，随着量子数𝑛 及𝑙 的增大，精细分裂迅速减小.
   2. 双重能级中，具有较高$J$ 值的能级，能量较高.

氢原子光谱的精细结构

1. Heisenber 的相对论修正:

   $$\begin{equation} \Delta E_r = -\frac{R h c \alpha^2 Z^4}{n^4} \left( \frac{n}{l + 1/2} - \frac{3}{4} \right) \end{equation}$$

2. Dirac 的自旋-轨道耦合修正:

   $$\begin{equation} \Delta E_{ls} = \frac{R h c \alpha^2 Z^4}{2 n^3} \frac{j(j + 1) - l(l + 1) - s(s + 1)}{l(l + 1/2)(l + 1)} \end{equation}$$

3. 氢原子总能量:

   $$\begin{equation} E_{nls} = E_n + \Delta E_r + \Delta E_{ls} = -\frac{R h c Z^2}{n^2} - \frac{R h c \alpha^2 Z^4}{n^3} \left( \frac{1}{j + 1/2} - \frac{3}{4 n} \right) \end{equation}$$ $$\begin{equation} = -\frac{m_e c^2 (Z \alpha)^2}{2} \left[ 1 + \frac{\alpha^2 Z^2}{n^2} \left( \frac{n}{j + 1/2} - \frac{3}{4} \right) \right] \end{equation}$$

   对于同一n，j相同的能级是简并的

4. Lamb 移位:
   (1) 真空极化：交换虚光子产生的虚正负电子对 对原子核电荷有屏蔽作用。
   (2) 自能作用：电子运动产生和吸收虚光子使电子质量增加。